Votre confusion vient du fait que votre esprit (et le récepteur de la portée WX GUI) utilise une interpolation linéaire entre les échantillons.

Ce n'est pas vrai - dans votre cas, où la période du signal n'est pas un nombre entier d'échantillons, cela devient évident par le fait que les choses ne semblent pas très sinusoïdales. Ils le sont toujours (je le promets;)).

Pensez-y comme ceci: à exactement 16 kHz échantillonnés avec 32 kHz, vous obtiendrez 2 échantillons par période, non? Donc, si ces échantillons se trouvent sur les extrema du cosinus, vous obtiendrez $ [+ 1 \, -1 \, +1 \, -1 \, \ ldots] $.

Avec 13,7 kHz pas si loin de là, vous obtenez "surtout" des signes alternés, mais à chaque fois et tant d'échantillons, vous "frappez" toujours la même moitié supérieure ou inférieure d'un cosinus deux fois. C'est pourquoi les choses semblent irrégulières.

Les choses sont en parfait état, belle forme! J'ai créé un cahier Jupyter rapide pour illustrer. Si vous n'avez pas le temps de le lire, voici les points à retenir:

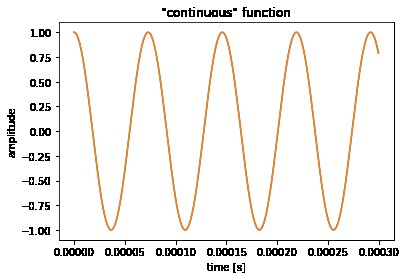
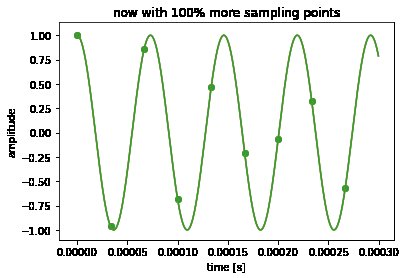
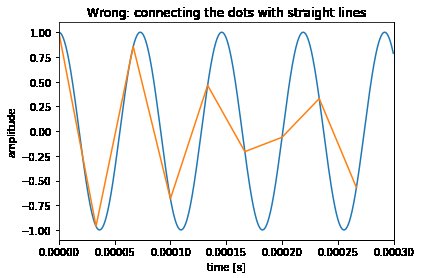
Ce que vous devez faire, mentalement, est d'interpoler en utilisant une fonction $ \ mathrm {sinc} $ comme interpolateur. (Je l'ai fait dans la version améliorée du cahier avec les plus grandes images dans la dernière partie.)

Le fait est que même si cela ne lui ressemble pas, ces " Les échantillons "dentelés" d'une oscillation de 13,7 kHz sont toujours à 100% de cette oscillation et contiennent toutes les informations du signal continu. Super!